Наш проект направлен на исследование и внедрение различных подходов к решению математических задач. Мы предлагаем уникальный метод, который сочетает теоретические знания с практическими навыками, необходимыми для успешного решения разнообразных математических задач.

Тип: Образовательный проект

Идея проекта: Идея проекта заключается в создании учебной среды, способствующей систематическому освоению стратегий решения математических задач, а также их успешному применению на практике.

Цель проекта: Цель проекта — обучить учащихся и всех желающих эффективным стратегиям решения математических задач, развить их логическое мышление и уверенность в своих математических способностях.

Проблема: Многие учащиеся испытывают затруднения при решении математических задач из-за неудовлетворительных знаний стратегий и методик их применения.

Целевая аудитория: Школьники, студенты, люди, желающие улучшить свои навыки решения математических задач

Задачи проекта: 1. Изучение различных стратегий решения математических задач. 2. Практическое освоение методик применения стратегий на разнообразных типах задач. 3. Проведение тематических мастер-классов и тренингов по развитию навыков решения задач.

Роли в проекте: Преподаватель, методист, ученик

Ресурсы: Учебные пособия, материалы для проведения тренингов, презентационное оборудование, печатные задачники

Продукт: Онлайн-курс по развитию навыков решения математических задач с интерактивными упражнениями и заданиями, учебные пособия и методические рекомендации.

Введение

Описание темы работы, актуальности, целей, задач, новизны, тем, содержашихся внутри работы. Контент доступен только автору оплаченного проекта

Основные стратегии решения математических задач

Обзор основных стратегий решения математических задач, включая методы анализа, логического мышления и систематического подхода к задачам различной сложности. Контент доступен только автору оплаченного проекта

Практическое применение стратегий в решении задач

Исследование способов применения стратегий решения математических задач на практике. Анализ конкретных примеров и задач для эффективного использования стратегий. Контент доступен только автору оплаченного проекта

Методики обучения стратегиям решения задач

Рассмотрение различных методик и подходов к обучению стратегиям решения математических задач. Оценка эффективности различных образовательных подходов. Контент доступен только автору оплаченного проекта

Тематические мастер-классы по решению задач

Анализ проведения мастер-классов и тренингов по развитию навыков решения математических задач. Описание форматов занятий и результатов обучения. Контент доступен только автору оплаченного проекта

Проблемы и трудности при решении математических задач

Исследование основных проблем, с которыми сталкиваются учащиеся при решении математических задач из-за недостаточных знаний стратегий и методик. Контент доступен только автору оплаченного проекта

Эффективные онлайн-курсы по решению математических задач

Обзор онлайн-курсов, предназначенных для развития навыков решения математических задач. Оценка интерактивных упражнений и методических материалов. Контент доступен только автору оплаченного проекта

Интерактивные упражнения для тренировки навыков решения задач

Исследование различных форм интерактивных упражнений, способствующих тренировке навыков решения математических задач. Описание принципов эффективной тренировки. Контент доступен только автору оплаченного проекта

Развитие логического мышления через решение задач

Анализ влияния решения математических задач на развитие логического мышления у учащихся. Оценка взаимосвязи между логикой и математикой. Контент доступен только автору оплаченного проекта

Инновационные подходы к обучению математике

Исследование новаторских методов и подходов к обучению математике, включая использование технологий, игровых элементов и интерактивных заданий для эффективного обучения. Контент доступен только автору оплаченного проекта

Роль самостоятельной работы в освоении стратегий решения задач

Анализ значимости самостоятельной работы и практических занятий в освоении стратегий решения математических задач. Исследование влияния самостоятельной работы на успех обучения. Контент доступен только автору оплаченного проекта.

Мастер-класс по решению нестандартных задач с использованием логических таблиц

Мастер-класс «Решение нестандартных задач с использованием логических таблиц»

Решение логических задач — это очень увлекательное занятие. В них, на первый взгляд, отсутствует математика: нет чисел, функций, треугольников, векторов, но присутствуют лжецы и мудрецы, истина и ложь. Тем не менее, дух математики проявляется здесь ярче всего — значительная часть решения любой математической задачи заключается в тщательном анализе условий и распутывании всех связей между объектами. Для этого помогают логические таблицы.

Оценить: 2665 0

Содержимое разработки

Мастер-класс по теме: «Решение нестандартных задач с использованием логических таблиц».

Научиться решать логические задачи на установление соответствий между элементами множеств с помощью таблиц;

Развивать логическое мышление, мыслительные навыки (анализ, синтез, сравнение, обобщение) и творческие способности;

Формировать культуру общения и сотрудничества при активных формах работы.

I этап. Озвучивание темы, целей, задач урока и мотивация учебной деятельности.

II этап. Подготовка к изучению нового материала через актуализацию базовых знаний.

III этап. Ознакомление с новым материалом.

IV этап. Подведение итогов занятия.

V этап. Постановка домашнего задания.

Здравствуйте, уважаемые коллеги!

Скажите, почему львы едят сырое мясо?

Конечно, потому что они не умеют готовить!

Сколько конфет можно съесть натощак?

Из школьного курса вы, наверное, знаете, что в середине прошлого века Грегор Мендель проводил свои опыты, пытаясь разгадать одну из тайн жизни. Он скрещивал сорта гороха жёлтого и зелёного цвета, что привело к открытиям законов наследования и возникновению генетики, объясняющей эти законы.

На вашем столе лежат горошины разного цвета. Узнайте, сколько горошин поместится в стакан? (Можете проверить.) На самом деле правильный ответ: «Нисколько!», — «Почему?» — «Потому что горошины не могут сами войти в стакан!».

Какие предложения вы можете составить?

НА ПОЛЕ ОН КОСИЛ ТРАВУ ПОЛЯ КИПЕЛИ

НАПОЛЕОН КОСИЛ ТРАВУ ПОЛЯКИ ПЕЛИ

Получается, одна и та же запись содержит два разных текста. Такой текст, который можно прочитать по-разному, называется палиндромом. Такая же особенность присутствует и в генетическом тексте ДНК.

Палиндромы встречаются в лингвистике при расшифровке мёртвых языков, а также в алгебре при решении возвратных уравнений.

Подобные шутливые и серьёзные логические игры и задачи наверняка были частью нашей жизни. Верно? Любили ли вы в детстве логические игры и задачи? Какие? А сегодня? Чем они хороши? Логические игры и задачи прекрасны тем, что заставляют думать даже самых ленивых. Сегодня я хочу вспомнить о них.

Есть люди, которые быстро решают такие задачи.

Их мозг сразу освещает все хитросплетения, и они быстро находят правильный ответ. Удивительно, что при этом они говорят: «Ну это же очевидно, ясно», и легко распутывают клубок противоречивых утверждений. «Действительно, все ясно», — говорит слушатель, огорченный тем, что сам не увидел очевидного решения. Согласитесь, такое же чувство часто возникает у нас при чтении детективов.

Решение логических задач очень увлекательно. В них вроде бы нет математики: ни чисел, ни функций, ни треугольников, ни векторов, но присутствуют лжецы и мудрецы, истина и ложь. Тем не менее, дух математики проявляется здесь ярче всего — значительная часть решения любой математической задачи заключается в тщательном анализе условий и распутывании всех связей между объектами.

Интересно отметить, что решение задач чисто логического типа в некоторой степени моделирует решение научных проблем. Перечислите основные этапы.

Мы сталкиваемся с множеством более или менее разобщённых данных;

Выдвигаем рабочую гипотезу;

Проверяем правильность гипотезы;

В конце концов приходим к заключению, которое безупречно согласуется с начальными условиями;

Проверяем выводы, чтобы убедиться, что они однозначны.

Почему некоторые люди делают открытия, а другие нет? Это происходит потому, что у них есть интуиция, творческое мышление и сохраняется детский взгляд на мир. Все открытия, которые сделали Луи Пастер, Архимед и Колумб, уже существовали, но только они смогли их заметить. Логика также помогает видеть необычное в обычном.

Сегодня мы узнаем, как можно решать логические задачи.

Один из способов решения логических задач — метод рассуждения. Давайте решим следующую задачу.

1. В трёх мешках находятся мука, крупа и сахар. На первом мешке написано «крупа», на втором — «мука», а на третьем — «крупа или сахар». Известно, что содержимое ни одного из мешков не соответствует надписи на нём.

Что в каком мешке находится?

Прочитайте вслух первую задачу. Подумайте, какая фраза является ключевой. Как будем рассуждать? Кто продолжит рассуждения? Все согласны? Запишите ответ.

2. Аня, Женя и Нина узнали свои оценки за контрольную работу по математике. Учитель сказал: «Плохих оценок нет. У вас троих они разные. У Ани не «3», у Нины не «3» и не «5»».

Кто какую оценку получил?

Прочитайте вторую задачу. Рассуждая аналогично, решите её самостоятельно.

Задача №1. На мастер-класс приехали учителя, преподающие разные предметы. Нам нужно познакомиться с пятью из них. Известно, что их имена А, Б, В, Г и Д. Один из них учитель математики, другой — учитель географии, третий — учитель физики, четвёртый — учитель биологии, пятый — учитель истории. Они рассказали о себе следующее:

В и Г не используют учебник математики в своей работе.

Г и Б живут в одном доме с учителем физики.

А и Г подарили учителю истории красивую вазу.

Б и Г помогали учителю географии готовить открытый урок.

Б и Д по субботам встречаются у учителя истории, а учитель физики по воскресеньям приходит в гости к А.

Кто из них преподаёт какой предмет?

Прочитайте задачу. Попробуйте её решить. Почему не получается? Сравните с предыдущими задачами: чем она отличается от них?

Мысленно проследить нить рассуждений трудно. Здесь очень легко запутаться. Для решения таких задач гораздо удобнее свести анализ к системе записей. Один из методов анализа — построение таблицы, учитывающей все возможные варианты. В математике есть приём, который значительно ускоряет, почти автоматизирует решение таких задач — это логические таблицы.

Между элементами каких множеств нам нужно установить соответствие? (имя и предмет).

Назовите имена (вписать), перечислите предметы (вписать). Есть ли в условии ключевая фраза, которая поможет вам начать? Может быть, о ком-то из учителей известно больше, чем о других (например, о Г). Давайте прочитаем, что известно о Г, и, делая выводы, заполним таблицу с помощью знаков + и –.

Вот пример такой таблицы:

35 методик и способов решения сложных задач

35 методик и способов решения сложных задач

Все команды и организации сталкиваются с трудностями по мере роста. Возникают проблемы, связанные с недопониманием или решением критически важных бизнес-задач. Вы можете столкнуться с вызовами в области роста, дизайна, взаимодействия с пользователями и даже культуры и благополучия команды. Вкратце, методы решения проблем должны быть в арсенале умений каждой команды.

Методы решения проблем предназначены для помощи группе или команде в процессе сначала выявления проблем и вызовов, разработки возможных решений, а затем оценки наиболее подходящих.

Найти эффективные решения сложных проблем нелегко, но используя правильные процессы и техники, вы можете помочь своей команде стать более эффективной в этом процессе.

Так как же разработать стратегии, которые вовлекают и наделяют вашу команду способностью эффективно решать проблемы?

В этом посте в блоге мы делимся серией инструментов для решения проблем, которые вы можете использовать на следующем воркшопе или командном собрании. Вы также найдете советы по упрощению процесса и способам вовлечения других в решение сложных задач.

Приступим!

• Как выявить проблемы?
• Как определить правильное решение?
• Советы для более эффективного решения проблем
• Полные методы решения проблем
• Техники решения проблем для выявления и анализа
• Техники решения проблем для разработки решений
• Разогревающие упражнения для решения проблем
• Заключительные упражнения для процесса решения проблем

Как выявить проблемы?

Прежде чем перейти к поиску правильного решения для данной проблемы, сначала необходимо идентифицировать и определить проблему, которую вы хотите решить.

Здесь важно четко сформулировать, в чем заключается проблема, и дать возможность вашей группе сделать то же самое. Помните, что у каждого в группе могут быть разные точки зрения, и согласование необходимо, чтобы помочь группе двигаться вперед.

Точное выявление проблемы также требует, чтобы все члены группы могли вносить свой вклад в открытой и безопасной обстановке. Людям может быть страшно выступать и делиться, особенно если проблемы или вызовы являются эмоциональными или личными. Постарайтесь создать психологически безопасное пространство для таких обсуждений.

Помните, что анализ проблемы и дальнейшее обсуждение также важны. Не уделив достаточно времени на полный анализ и обсуждение вызова, можно разработать решения, которые не подходят по назначению или не решают основную проблему.

Успешное выявление и анализ проблемы означает помощь группе через действия, направленные на четкое и честное выражение своих мыслей и получение полезных инсайтов.

С этими данными вы можете сформулировать заявление о проблеме, которое четко описывает проблему, которую вы хотите решить, а также цель любого процесса, который вы предпринимаете для решения этой проблемы.

Как определить правильное решение?

Поиск решений является конечной целью любого процесса. Сложные организационные проблемы можно решить только с помощью подходящего решения, но его обнаружение требует использования правильного инструмента для решения проблем.

После того, как вы исследовали проблему и обсудили идеи, необходимо помочь команде обсудить и выбрать правильное решение. Инструменты и методы консенсуса, такие как приведенные ниже, помогают группе исследовать возможные решения, а затем проголосовать за лучшее. Это отличный способ использовать коллективный интеллект группы для достижения отличных результатов!

Помните, что процесс часто является итеративным. Великие решатели проблем часто тестируют жизнеспособное решение в ограниченном масштабе, чтобы увидеть, что работает. Хотя вы можете не найти правильное решение с первой попытки, приведенные ниже методы помогают командам выбрать наиболее вероятное успешное решение, оставляя место для улучшений.

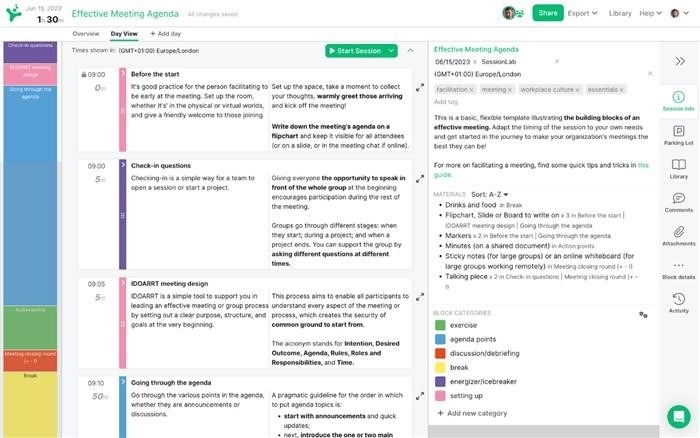
Каждый эффективный процесс решения проблем начинается с повестки дня. Хорошо структурированный воркшоп — один из лучших методов для успешного руководства группой от исследования проблемы до внедрения решения.

В SessionLab легко перейти от идеи к полной повестке дня. Начните с перетаскивания основных действий по решению проблем на место. Добавьте время, перерывы и необходимые материалы, прежде чем поделиться повесткой дня с коллегами.

Полученная повестка дня будет вашим руководством к эффективной и продуктивной сессии по решению проблем, которая также поможет вам оставаться организованными в день мероприятия!

Советы для более эффективного решения проблем

Деятельность по решению проблем представляет собой лишь одну часть головоломки. Даже самый лучший метод может оказаться неэффективным без внимательного подхода и качественного содействия команды.

Рассмотрим несколько советов по решению проблем, которые вы можете применить к любому процессу, чтобы сделать его успешным!